Séamas Ó Brógáin
This is a revised version (completed in September 2006) of the paper “Typographic measurement: A critique and a proposal,” published in Professional Printer: Journal of the Institute of Printing, vol. 27, no. 5 (1983), p. 9–14. It is reproduced here with the permission of the Institute of Paper, Printing and Publishing.
Parts of this web page require mathematical mark-up (MathML) to display properly. Browsers that conform to this standard include Firefox and Safari; those that do not work include Chrome, Chromium, Internet Explorer, and Opera.
First introduced more than two hundred years ago, the point system has been universally used for the last hundred years for expressing the size of type. With the adoption of personal computers from the 1980s, this system has been carried over to computer-assisted editing, typesetting, and design. From its inception, however, it has had two significant drawbacks:
The continued use into the computer era of this doubly incoherent system makes for particular difficulties in design and page layout. With the “body size” system generally, the object nominally measured—in whatever units—is not visible and cannot usually be measured on the printed page; with digital type it has no real existence. At the same time the designer, typically working in millimetres, is compelled to mix millimetres with points in order to specify type size or line-spacing.
Postscript fonts are typically created on a grid 1,000 units deep, and Truetype fonts on a grid 2,048 units deep, within which the typeface designer chooses where to place the baseline and mean line, thus establishing the relationship between nominal size and x height for that typeface. (The newer Opentype format contains either Postscript or Truetype outlines, and the proposed Open Font format is in turn based on Opentype.) When type is used in an application it is the whole of this grid that is given the nominal (point) size.
For hundreds of years, typesetting involved the manipulation of lead type—small blocks of lead with the image moulded on one end—which were picked up, one for each character, and assembled by hand. Each piece of type was a solid object with a measurable vertical dimension; and it was this “body size” that acted as nominal type size. From the end of the nineteenth century, with the invention of the Monotype and Linotype machines, this process was mechanised, but it still produced lead type (either single characters or complete lines) of a fixed depth.
Today there is no lead type; the dozen or so familiar book types of the early twentieth century have given way to thousands of digital types; and the printing craftsman has been replaced by a graphic designer who has never seen lead type and may not even know what the measurement given in points refers to. (It is often stated that it is a measurement of the overall size—the distance between the ascender line and the descender line—which is not correct.)
From the nominal size of metal type, printers and their customers referred to the printed image as “12-point type,” “10-point type,” and so on. There is no part of the printed image that can be measured and said to be 12 points or 10 points, though printers and others familiar with the commonly used typefaces had a reasonable idea of what they would look like in different sizes. The measurement from one baseline to the next will produce this figure, but only if the type is set solid, i.e. if there is no “leading” or additional line-spacing, but this is something that cannot be assumed; and it still leaves us with a dimension not connected except in a very loose way with the visual size.
For the printer the most important consideration was that the different pieces of lead type should fit together exactly, regardless of the design of the type or the foundry in which it had been cast. It was this that provided the impetus for the development of the point system when printers began to buy type from different typefounders, rather than casting their own.
A number of French inventors in the eighteenth century had the idea of a measurement system based on a very small unit that could be the lowest common denominator of a range of related sizes. All but the first (Sébastien Truchet in 1725) used one seventy-second of the contemporary inch—a reasonable choice for a duodecimal world. The inch, however, has had slightly different dimensions in different countries and at different times, and so therefore has the typographic point.
The unit proposed by the punch-cutter and typefounder Pierre-Simon Fournier (Fournier le Jeune) from 1737 was one seventy-second of the contemporary French inch, though this was not legally defined. The point was more precisely defined by the printer François-Ambroise Didot from about 1783 as of the pied du roi or royal foot, and this unit (≈ 0.376 mm), now generally known as the Didot point, came to be used generally throughout Continental Europe.1
The American point (generally called the Anglo-American point following its adoption in England from the end of the nineteenth century) was defined in 1886 by the Type Founders’ Association of the United States as cm (≈ 0.351 mm).2 The Monotype Corporation used its own definition of the Anglo-American point for its widely used typecasting machines (to facilitate its ingenious “unit” system), defined as 0.0007685 inch × 18 = 0.013833 inch (≈ 0.351 mm also).3
At the beginning of the computer era, the point used by the typesetting language Tex (from about 1978) was defined as inch, a novel formulation that produces a figure almost identical to the Anglo-American and Monotype points. With the introduction of the first Apple Macintosh computer in 1984 a monitor was provided that had exactly seventy-two pixels per vertical inch as well as a display system that showed text in various typefaces and at actual size (“what you see is what you get”), so introducing the computer point, of exactly one seventy-second of a standard inch (25.4 mm) or approximately 0.353 mm—the point now generally used in digital typography. Because the Postscript page description language was introduced shortly afterwards, this unit is also called the “Postscript point.”
There have been two false starts in the reform of the point system. When the first modern efforts to “metricate” typography were made, the proposers did just that: they converted the dimensions of lead type from points to millimetres, and generally also rationalised the range of sizes. The most notable proposal was that of the Dutch printer Adolf Stork—later director of the Stadsdrukkerij, Amsterdam—whose scheme was implemented in a number of Dutch, French and German printing houses.4 A similar approach was adopted by the British Federation of Master Printers, resulting in a British standard, BS 4786 (1972), which was simultaneously submitted to the International Organization for Standardization as a possible international standard; but it was not implemented anywhere and was later withdrawn.5
National standards were subsequently adopted (or confirmed) in some countries that disregarded the developing consensus that some aspect of the visual image should be the basis of nominal type size. A Japanese standard dating from 1962 and confirmed in 2006 specifies the use of the millimetre (alongside the American point, which it defines as 0.3514 mm), though it also introduces a pseudo-unit, the Q (for “quarter”), as a special name for 0.25 mm.6 (By “pseudo-unit” I mean a special name given to what is merely a fraction of an existing standard unit.) Such standards, by specifying dimensions in millimetres, may be perceived as eliminating the use of the point but are in fact irrelevant, as designers, typesetters and other computer users in all countries use the same computers and applications and are thereby locked in to the computer point.
The other proposed reform, and the first based on a visual aspect, was pioneered from about 1966 by the Austrian-British graphic designer and teacher Ernest Hoch, originally under the auspices of the International Council of Graphic Design Associations (ICOGRADA). Hoch and his colleagues proposed the height of the capital letters in millimetres, called H-height, as the nominal size.7 (Capital height is normally the same as ascender height, though in some typeface designs it is a little less.) Though this was a breakthrough, bringing in for the first time the concept of a measurable dimension of the printed character, it still failed to indicate the true visual size while at the same time it alienated those who wished to retain mechanical (body) size. Perhaps an explanation for this false start is to be found in the historical priority and significance of capital letters. For the purposes of measurement, however, what we are concerned with is the selection of a single dimension to act as the nominal size of type and as the basis for equating and aligning different typefaces. No historical or cultural judgements are involved: it is simply a measurement of size.
In 1975 the International Organization for Standardization established a “Typographic Measurement” working group, of which Hoch was appointed convener, and this became the battleground between those who wished to push ahead for a visual dimension and those who wished to retain body size—under a variety of names—despite the rapidly changing technology.8 Draft standards were drawn up, based on the H-height approach, but agreement could not be reached, and the project was suspended in 1982 and formally ceased in 1984.
The revised German standard of 1999 adopts the approach abandoned in the British standards process by specifying schriftgröße (“type size,” i.e. body size) in millimetres but goes further by proposing that the manufacturers of fonts make capital height a fixed fraction of this size for all typeface designs, namely 66.7 per cent (i.e. ) for the Didot point system or 70.9 per cent for the Anglo-American point system—though computer applications use neither of these units but rather the computer point.9 This is clearly an attempt at reconciling the conflicting requirements of a system based on the now non-existent body size and one based on some visual aspect. A general implementation of this system would require that all typeface designers and font manufacturers apply this formula to newly manufactured fonts; and it could not be applied to the millions of copies of thousands of fonts already in use.
Special unit, or special name? Despite the weight of tradition, there is no technical need for any special measurement unit in typography, with or without a special name. The 16th General Conference on Weights and Measures (1979) resolved “that the proliferation of special names represents a danger for the Système International d’Unités and must be avoided in every possible way . . .”10 What we are dealing with is a simple linear measurement. Type size and spacing can be measured perfectly well in millimetres, the same unit used for the other dimensions on a page.
Numerous writers over the years have had to resort to complex explanations to accommodate the fact that what is called the “size” of type is not really the size at all. The following example is from the classic Introduction to Typography by Oliver Simon:
A further examination of [specimens of twenty-three typefaces] shows very considerable differences in the size of the actual type face on the 12-pt. body . . . Plantin and Times, for instance, are, in relation to others, so large on their bodies that whilst 12 pt. is the norm for almost all the types exhibited, the equivalent could well be 11 pt. in their case . . . This ‘largeness’ on the body is measured first in terms of the height of the non-ascending and non-descending lower-case letters, e.g. x (hence the term ‘x-height’), and secondly, the width of the m (which determines the ‘set’).11
Where objective comparisons of sizes were required, a small number of writers accepted the logical conclusion and based these explicitly on the x height, as for example:
The typefaces of the various systems are different in their image size for the same type size . . . In order to provide an objective comparison, the lower-case letters have been brought to a unified dimension.12
One area in which an objective comparison of type size has a particular importance is the measurement of legibility. Unlike previous studies, which had used only a comparison of “point sizes” and were therefore questionable, the Swedish researcher Bror Zachrisson employed “visual size,” which he defined as “x-height measured in mm multiplied by the mean width of the letters.”13 (A more exact definition of visual size would certainly have to take into account the width of the letters, but this has been decided beforehand by the type designer; the only dimension under the control of the user of a typeface is the vertical one, with the horizontal dimension changing accordingly.)
In the illustration below, the first word in each line (in Garamont) is 24 pt, while the second word (in Helvetica) is 24 pt in the first line, 22 pt in the second line, and 18 pt in the third line. According to the present system, the two words in the first line are the same size. Clearly, however, they are not.
According to those who advocate the use of capital height as nominal size, the two words in the second line should be equated. Though this is an improvement, it is hard to see how it could be regarded as an acceptable solution.
One has only to scan any page of text (or the text of this web page) to see that what constitutes the text is rows of varying character shapes that, in combination, present to the eye a quite uniform pattern—a pattern created by the x height. The protruding ascenders and descenders, and occasional capital letters, are not sufficient to break this pattern. Here, surely, is the “size” of the type. The conclusion to be drawn is that x height, given in millimetres, should be used for describing and specifying type size. The concept of a standardised range of sizes is redundant, as digital type can be scaled up or down to any size.
It is necessary to accommodate two other dimensions: line-spacing and capital height. Though the former may correspond to the historical body size, and the latter corresponds to the dimension chosen for the earlier reform proposal, they are included here for objective reasons, in that it may be necessary to specify them independently. Because of the strength of the argument in favour of the x height as nominal size, these should be regarded as minor complications rather than as counter-arguments.
Line-spacing. The specification for type size combined with line-spacing has traditionally used a simple notation, namely the two figures separated by an oblique stroke, as for example 10/12 pt (or simply 10/12). An increase in line-spacing was originally achieved by adding thin strips of lead between the lines and later by casting (for example) 10-point type on a 12-point body, as a result of which this notation is verbalised as “ten on twelve (point).” There is no reason not to use the same notation when giving dimensions in millimetres, as for example 1.5/4.
Capital letters. There are certain circumstances in which capital letters are used alone, without their corresponding lower case (or without necessarily having a lower case). An unambiguous solution would be to enclose the figure for capital height in parentheses; and this too could be combined if necessary with the figure for line-spacing, as for example (5)/7.5.
In digital fonts it is possible for the type designer or manufacturer to specify explicitly the dimension of the x height for a particular typeface (in terms of the number of em units within the design grid); but whether this is done or not it is also feasible for applications to be supplied with the height of the actual letter x. Unfortunately, applications would have to be rewritten to allow this dimension to be used as the nominal size, and for this to happen it would be necessary for a consensus or at least a certain demand for such a feature to have arisen. On the other hand, this feature might at first be provided as an option rather than as the default method; and it could be introduced piecemeal in individual applications, without waiting on any global or synchronised changeover. Most importantly, no changes would be required to existing digital fonts.
Fonts in web pages. In cascading stylesheets (used in conjunction with the mark-up language for web pages) it is already possible to dispense with the point, as type size (and line-spacing) can be specified in millimetres, thus eliminating one half of the problem. What is specified, however, is the em square, defined as “an abstract square whose height is the intended distance between lines of type in the same type size”—in other words, the historical body size.14 This is a non-existent dimension as far as the user is concerned.
It is gratifying to note in the same specification the statement that “the subjective apparent size and legibility of a font are less dependent on their ‘font-size’ value than on the value of their ‘x-height’, or, more usefully, on the ratio of these two values,” for which the term aspect value is introduced. However, the ability to specify type size in terms of this value is not offered.
The system described above, based on the requirements of the Roman alphabet, can be applied to other scripts also, which for this purpose it is convenient to divide into three categories.
1. The Greek and Cyrillic alphabets have a structure similar to the Roman alphabet in having distinct capital and lower-case letters.
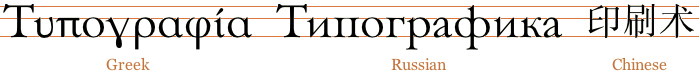
2. Chinese, Japanese and Korean characters—being essentially square and of a uniform height, as well as relatively complex—lend themselves to being equated with capital letters for the purposes of alignment and measurement. Traditional publishing practice has generally been to centre such characters vertically (i.e. between baselines), though computer applications, including web browsers, normally use the base-alignment model.
3. Other scripts—including Arabic, Hebrew, and the scripts of India and south-east Asia—require separate decisions, based on expert knowledge; but the criterion in each case should be the same: for the nominal size a dimension should be chosen that best represents the visual size. This would be aligned when necessary with the x height (or, exceptionally, the capital height) of the Roman alphabet.
Comments to sob@iol.ie
  |